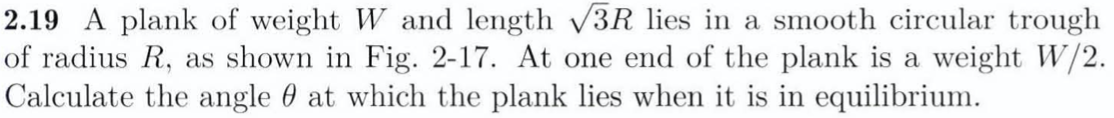
Since I’ll be using principle of virtual work with the impossible triangle trick, I need to know how the diagram would move under small perturbation.

Now, the first thing to notice is that that the angle between the two ends of the rod would remain the same, $120^\circ$, since the rod will be sitting on top of the circle.

Next, notice that the two ends of the rod would move the same distance along the circle, since if you move one end of the rod by $R\,d\theta$, the other end of the rod would move $R\,d\theta$

For the principle of virtual work to work, we need two information.

1. How the center of mass(COM) of the rod changes
2. How the weight $W/2$ moves

Fortunately, we can use the two end points to get both of them, and since the two end points always move the same distance, that should make our job considerably easier.

If we call our position vector of the left end of the rod $\vec{a}$ and call the right end of the rod $\vec{b}$, the COM of the rod would be $\frac{\vec{a} + \vec{b}}{2}$

For the weight $W/2$, the position vector is just $\vec{b}$

Now, if we want to find the change of the position vector, for the COM it’s $\frac{\Delta\vec{a} + \Delta\vec{b}}{2}$, and for the $W/2$, it’s $\Delta\vec{b}$

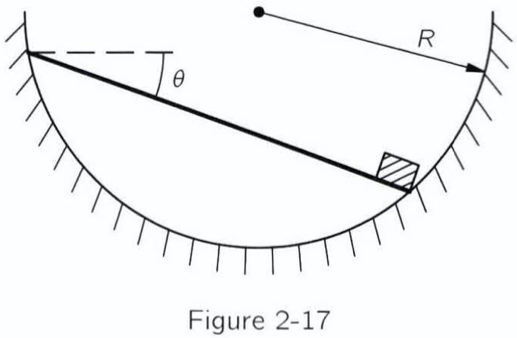
Here is where the impossible triangle comes into play, we imagine the rod moving a very small distance, in fact an infinitesimally small distance, along the circle, bit like the circle above, but infinitely smaller.

Now, due to the property of this triangle, we also imagine it as a tangent to the whole outer circle. Then parameterize it with the angle the circle makes with the vertical axis.

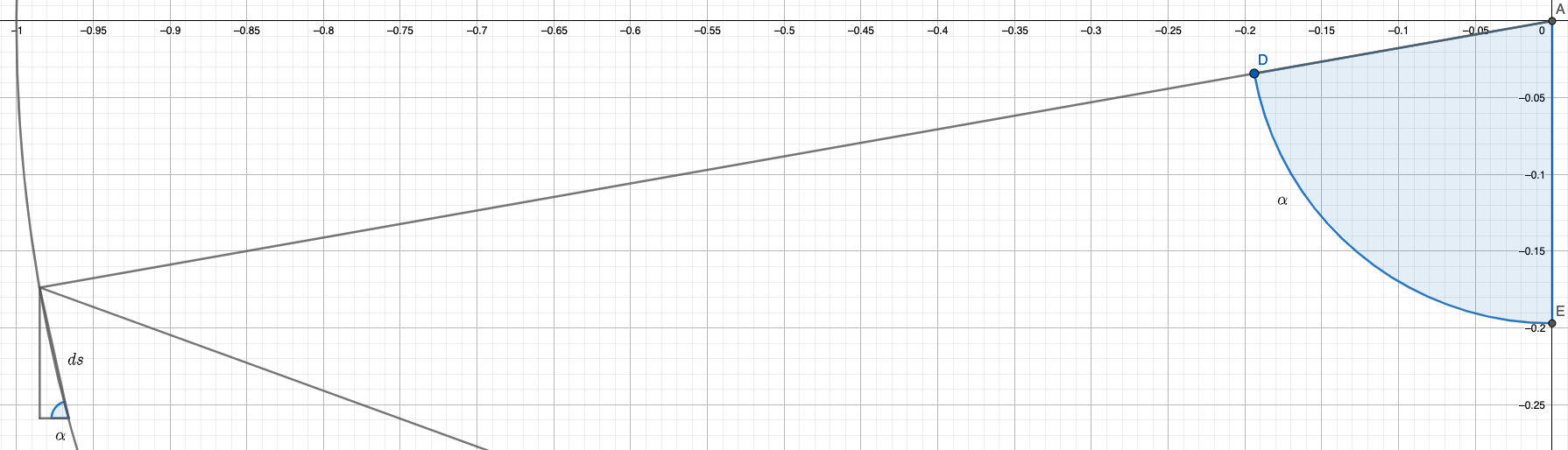
We’ll worry about how to get $\theta$ from $\alpha$ later, but you can figure it out yourself if you want to. (it’s not that hard)

Then parametrize the right end of the rod with respect to $\alpha$, and you’ll find that the angle of the small triangle will be $120^\circ - \alpha$ (I won’t draw the figure here, just keep in mind the angle between the two ends is $120^\circ$, and you can figure out the rest)

Finally, we need to choose a direction aka choose a sign. For convention, we’ll choose down as minus, and up as positive.

We’ve finished all the setup we need. Since the distance required for the virtual work calculation is the vertical distance, we take the height changed by the small distances at the two ends, multiply by the appropriate weights, add it all up, set it zero, and start the usual algebra.

Height changed on the left end: $-ds\sin (\alpha)$

Height changed on the right end: $ds\sin (120^\circ - \alpha)$

Virtual work on the COM of the rod: $W\frac{1}{2}(ds\sin (120^\circ - \alpha) - ds\sin (\alpha))$

Virtual work on the $W/2$ weight: $\frac{W}{2}ds\sin (120^\circ - \alpha)$

Total work

\[\frac{W}{2}ds(\sin (120^\circ - \alpha) - \sin (\alpha) + \sin(120^\circ - \alpha)) = 0 \\ 2\sin (120^\circ - \alpha) = \sin (\alpha)\]

We need to solve this equation. You can either use the sin addition formula or be lazy like me and ask wolfram alpha.

For the final step, how to find $\theta$ from $\alpha$

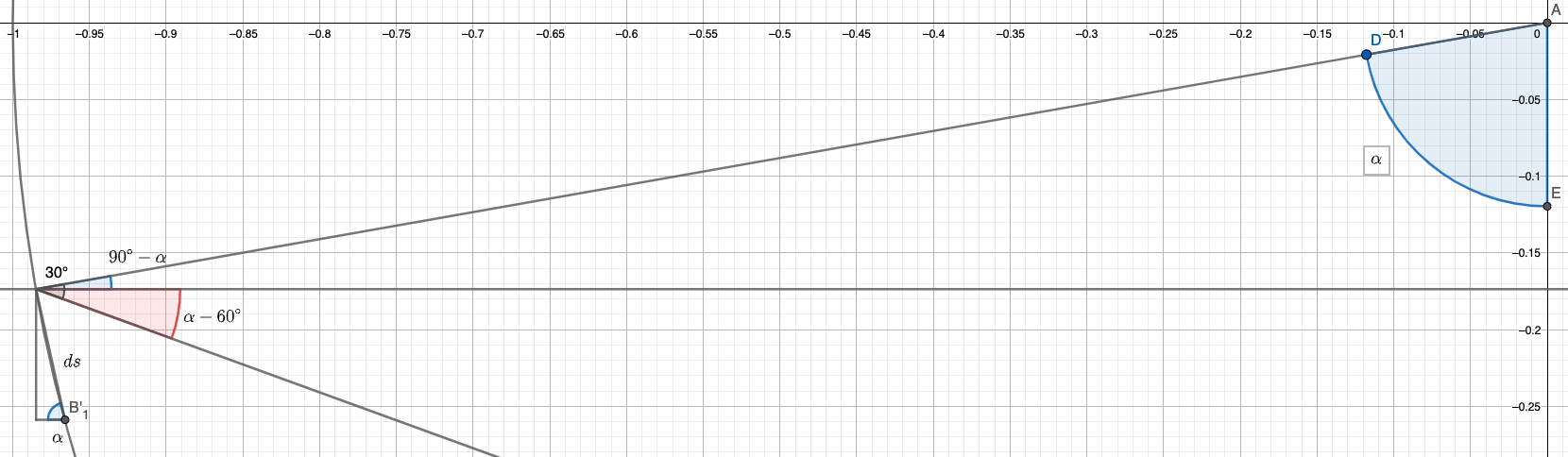
I’m sure you can fill in the rest